Cómo generar una función del mismo orden y otros pensamientos sobre la revisión de pares

Publicado el por

La academia tiene cosas curiosas. Por ejemplo uno de los tesoros guardados en más alta estima por la ciencia moderna es la identidad secreta de los pares que evalúan los artículos que los otras personas escriben. Lo de la identidad secreta puede hacerlos sonar a emocionantes súper héroes pero para los autores de artículos neófitos, como yo, sus comentarios suelen ser casi otro problema de investigación que ameritaría una tesis aparte. Mi comentario va a que, por más secreto que sea el proceso, dada la naturaleza de mi investigación, tengo un grupo bien cerrado de personas (tres) que, creo, pudieron ser los posibles referees de uno de mis papers.

No sé cómo tomarán las correcciones los autores senior de artículos científicos, pero en mi caso cada comentario de los referees en uno solo de mis papers es como si fuera una estocada y me alborota la gastritis. Al comienzo no fue así, creí que podía resolver sus cuatro correcciones principales fácilmente (las otras, que hubo más, eran de estilo y typos); pero con el correr de los días, al ver que no entiendo sus apreciaciones y cuando las entiendo no sé cómo solucionarlas, mi percepción se está convirtiendo rápidamente en que la corrección no es cosa sencilla. O tal vez sí y me estoy dejando abrumar.

La verdad a mí jamás se me habrían ocurrido esas correcciones que me hicieron así que de veras agradezco que me las hayan hecho evidentes. Pero duele un poco en el ego por varias razones que no mencionaré. Una amiga, quien tiende a ver las cosas siempre por el lado positivo, me planteó una idea diferente para solucionar parte de mi dilema interno de sentirme minúsculo: «Míralo por el otro lado —me dijo—: existen pocas personas en el mundo que pueden corregir lo que tú haces». Esa percepción es interesante porque me resuelve en mucho el golpe al ego (y lo acepto, ese me dolió bastante)… la cosa es que el ego arreglado no me soluciona el problema matemático, lo que necesito resolver para ver mi artículo publicado :-/.

En fin, con base en eso quiero aquí mostrar un argumento muy simple de dos funciones del mismo orden: Sean g(x)=\frac{x-1-\log x}{x} y f(x)=\frac{(x-1)^2}{2}. El referee dice que las dos funciones son del mismo orden cuando x\rightarrow1, cosa que es fácilmente verificable, como procederé a mostrar. Decir que las dos funciones son del mismo orden cerca de 1 es decir \lim_{x\rightarrow1}g(x)/f(x)=K, donde K es una constante diferente de 0. La razón es que si K se va para infinito en el límite entonces g crece más rápido que f y si K va para cero en el límite entonces f crece más rápido que g. Entonces, por definición de las dos funciones, tenemos que

\lim_{x\rightarrow1}g(x)/f(x)=\lim_{x\rightarrow1}\frac{2(x-1-\log x)}{x(x-1)^2}.

Ahora, llámeme superficial pero, como numerador y denominador van para 0 cuando x va para 1, la herramienta que yo uso para determinar este tipo de afirmaciones es la nunca bien ponderada pero siempre útil regla de L’Hopital, de la cual obtenemos:

\lim_{x\rightarrow1}g(x)/f(x)=\lim_{x\rightarrow1}g'(x)/f'(x)=\lim_{x\rightarrow1}\frac{2(1-1/x)}{(x-1)^2+2x(x-1)}.

Y esa última igualdad se puede re-escribir menos feo así:

\lim_{x\rightarrow1}\frac{2(x-1)}{x(x-1)^2+2x^2(x-1)}.

Luego, podemos volver a aplicar L’Hopital:

\lim_{x\rightarrow1}\frac{2}{(x-1)^2+2x(x-1)+4x(x-1)+2x^2}.

Y al final el límite es 2/2=1. La pregunta que me surge —la que inspira esta entrada— es cómo el señor referee encontró f(x) (sobre todo porque la encontró de tal manera que perjudica lo que quiero hacer con g(x)). Una vez tengo f(x) mostrar que las dos son del mismo orden cerca de 1 es fácil, pero ¿cómo encontrar f(x) originalmente? No lo he intentado pero la idea de «delvolverse» usando integración me suena un poco muy esotérica, la verdad.

5 pensamientos en “Cómo generar una función del mismo orden y otros pensamientos sobre la revisión de pares”

  1. Hola, seguro qeu un matemático (yo no lo soy) te dará una explicación mejor pero yo te doy la que se me ocurre
    1) está claro que lim g(x) vale 0 cuando x tiende a 1, por tanto para evitar que g(x)/f(x) valga 0 en ese límite (órdenes distintos) pues f(x) debe tener una raíz x = 1 (para que obtengas el 0/0)
    2) pero g'(x) vuelve a ser 0 en ese límite y sólo es distinto de 0 en la segunda derivada, por tanto f(x) debe ser dos veces derivable en x. Entonces f(x) = x-1 no te vale aunque tiene raíz 1 pues no es dos veces derivable en x (el límite tras la primera aplicación de lopital te daría 0) por tanto debe ser f(x) = (x-1)^2 que si es dos veces derivable y tiene raíz 1 y por tanto el límite de g(x) / f(x) te da un k > 0 concretamente 1/2. Ya has obtenido un f(x) del mismo orden que g(x). Como el límite de f(x) en la segunda derivada es 2, si deseas que el cociente te dé 1 en vez de 1/2 pues pones f(x) = (x-1)^2 / 2.

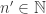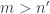  3. Solo una pequeña precisión: una función polinomial de orden n'\in\mathbb N es infinitamente diferenciable. Lo que pasa es que su derivada de orden m, para todo m>n' siempre va a ser 0. Pero el hecho de que la función asuma el valor 0 no la hace no diferenciable.

    Mejor dicho, una cosa es que la derivada sea nula y otra es que no sea diferenciable.

  5. La forma seguramente fue hacer Taylor, y quedarse con el primer termino no nulo que le quedó (por lo menos, yo haría eso)

Deja un comentario